函数是 Python 内建支持的一种封装,我们通过把大段代码拆成函数,通过一层一层的函数调用,就可以把复杂任务分解成简单的任务,这种分解可以称之为面向过程的程序设计。函数就是面向过程的程序设计的基本单元。
而函数式编程(请注意多了一个“式”字)—— Functional Programming,虽然也可以归结到面向过程的程序设计,但其思想更接近数学计算。
我们首先要搞明白计算机(Computer)和计算(Compute)的概念。
在计算机的层次上,CPU 执行的是加减乘除的指令代码,以及各种条件判断和跳转指令,所以,汇编语言是最贴近计算机的语言。
而计算则指数学意义上的计算,越是抽象的计算,离计算机硬件越远。
对应到编程语言,就是越低级的语言,越贴近计算机,抽象程度低,执行效率高,比如 C 语言;越高级的语言,越贴近计算,抽象程度高,执行效率低,比如 Lisp 语言。
?? 诞生 50 多年之后,函数式编程(functional programming)开始获得越来越多的关注。不仅最古老的函数式语言 Lisp 重获青春,而且新的函数式语言层出不穷,比如 Erlang、clojure、Scala、F# 等等。目前最当红的 Python、Ruby、Javascript,对函数式编程的支持都很强,就连老牌的面向对象的 Java、面向过程的 PHP,都忙不迭地加入对匿名函数的支持。越来越多的迹象表明,函数式编程已经不再是学术界的最爱,开始大踏步地在业界投入实用。也许继"面向对象编程"之后,"函数式编程"会成为下一个编程的主流范式(paradigm)。
4.1 什么是函数式编程
函数式编程就是一种抽象程度很高的编程范式,纯粹的函数式编程语言编写的函数没有变量,因此,任意一个函数,只要输入是确定的,输出就是确定的,这种纯函数我们称之为没有副作用。而允许使用变量的程序设计语言,由于函数内部的变量状态不确定,同样的输入,可能得到不同的输出,因此,这种函数是有副作用的。
? 函数式编程的一个特点就是,允许把函数本身作为参数传入另一个函数,还允许返回一个函数!
Python 对函数式编程提供部分支持。由于 Python 允许使用变量,因此,Python 不是纯函数式编程语言。
4.1.1 定义
简单说,"函数式编程"是一种"编程范式"(programming paradigm),也就是如何编写程序的方法论。它属于"结构化编程"的一种,主要思想是把运算过程尽量写成一系列嵌套的函数调用。
举例来说,现在有这样一个数学表达式:
(1 + 2) * 3 - 4传统的过程式编程,可能这样写:
var a = 1 + 2;
var b = a * 3;
var c = b - 4;函数式编程要求使用函数,我们可以把运算过程定义为不同的函数,然后写成下面这样:
var result = subtract(multiply(add(1,2), 3), 4);这就是函数式编程。
4.1.2 特点
函数式编程具有五个鲜明的特点。
① 函数是"第一等公民"
所谓"第一等公民"(first class),指的是函数与其他数据类型一样,处于平等地位,可以赋值给其他变量,也可以作为参数,传入另一个函数,或者作为别的函数的返回值。
举例来说,下面代码中的 print 变量就是一个函数,可以作为另一个函数的参数。
var print = function(i){
console.log(i);
};
[1,2,3].forEach(print);② 只用"表达式",不用"语句"
"表达式"(expression)是一个单纯的运算过程,总是有返回值;"语句"(statement)是执行某种操作,没有返回值。函数式编程要求,只使用表达式,不使用语句。也就是说,每一步都是单纯的运算,而且都有返回值。
原因是函数式编程的开发动机,一开始就是为了处理运算(computation),不考虑系统的读写(I/O)。"语句"属于对系统的读写操作,所以就被排斥在外。
当然,实际应用中,不做 I/O 是不可能的。因此,编程过程中,函数式编程只要求把 I/O 限制到最小,不要有不必要的读写行为,保持计算过程的单纯性。
③ 没有"副作用"
所谓"副作用")(side effect),指的是函数内部与外部互动(最典型的情况,就是修改全局变量的值),产生运算以外的其他结果。
函数式编程强调没有"副作用",意味着函数要保持独立,所有功能就是返回一个新的值,没有其他行为,尤其是不得修改外部变量的值。
④ 不修改状态
上一点已经提到,函数式编程只是返回新的值,不修改系统变量。因此,不修改变量,也是它的一个重要特点。
在其他类型的语言中,变量往往用来保存"状态"(state)。不修改变量,意味着状态不能保存在变量中。函数式编程使用参数保存状态,最好的例子就是递归。下面的代码是一个将字符串逆序排列的函数,它演示了不同的参数如何决定了运算所处的"状态"。
function reverse(string) {
if(string.length == 0) {
return string;
} else {
return reverse(string.substring(1, string.length)) + string.substring(0, 1);
}
}由于使用了递归,函数式语言的运行速度比较慢,这是它长期不能在业界推广的主要原因。
⑤ 引用透明
引用透明(Referential transparency),指的是函数的运行不依赖于外部变量或"状态",只依赖于输入的参数,任何时候只要参数相同,引用函数所得到的返回值总是相同的。
有了前面的第三点和第四点,这点是很显然的。其他类型的语言,函数的返回值往往与系统状态有关,不同的状态之下,返回值是不一样的。这就叫"引用不透明",很不利于观察和理解程序的行为。
4.1.3 好处
函数式编程到底有什么好处,为什么会变得越来越流行?
① 代码简洁,开发快速
函数式编程大量使用函数,减少了代码的重复,因此程序比较短,开发速度较快。
② 接近自然语言,易于理解
函数式编程的自由度很高,可以写出很接近自然语言的代码。
前文曾经将表达式 (1 + 2) * 3 - 4,写成函数式语言:
subtract(multiply(add(1,2), 3), 4)对它进行变形,不难得到另一种写法:
add(1,2).multiply(3).subtract(4)这基本就是自然语言的表达了。再看下面的代码,大家应该一眼就能明白它的意思吧:
merge([1,2],[3,4]).sort().search("2")因此,函数式编程的代码更容易理解。
③ 更方便的代码管理
函数式编程不依赖、也不会改变外界的状态,只要给定输入参数,返回的结果必定相同。因此,每一个函数都可以被看做独立单元,很有利于进行单元测试(unit testing)和除错(debugging),以及模块化组合。
④ 易于"并发编程"
函数式编程不需要考虑"死锁"(deadlock),因为它不修改变量,所以根本不存在"锁"线程的问题。不必担心一个线程的数据,被另一个线程修改,所以可以很放心地把工作分摊到多个线程,部署"并发编程"(concurrency)。
请看下面的代码:
var s1 = Op1();
var s2 = Op2();
var s3 = concat(s1, s2);由于 s1 和 s2 互不干扰,不会修改变量,谁先执行是无所谓的,所以可以放心地增加线程,把它们分配在两个线程上完成。其他类型的语言就做不到这一点,因为 s1 可能会修改系统状态,而 s2 可能会用到这些状态,所以必须保证 s2 在 s1 之后运行,自然也就不能部署到其他线程上了。
多核 CPU 是将来的潮流,所以函数式编程的这个特性非常重要。
⑤ 代码的热升级
函数式编程没有副作用,只要保证接口不变,内部实现是外部无关的。所以,可以在运行状态下直接升级代码,不需要重启,也不需要停机。Erlang) 语言早就证明了这一点,它是瑞典爱立信公司为了管理电话系统而开发的,电话系统的升级当然是不能停机的。
下面进行具体函数具体示例介绍:
4.2 高阶函数
高阶函数英文叫 Higher-order function。什么是高阶函数?我们以实际代码为例子,一步一步深入概念。
(1)变量可以指向函数
以 Python 内置的求绝对值的函数abs()为例,调用该函数用以下代码:
abs(-10) # 10但是,如果只写abs呢?

可见,abs(-10)是函数调用,而abs是函数本身。
要获得函数调用结果,我们可以把结果赋值给变量:
x = abs(-10)
x # 10但是,如果把函数本身赋值给变量呢?

结论:函数本身也可以赋值给变量,即:变量可以指向函数。
如果一个变量指向了一个函数,那么,可否通过该变量来调用这个函数?用代码验证一下:
f = abs
f(10) # 10成功!说明变量f现在已经指向了abs函数本身。直接调用abs()函数和调用变量f()完全相同。
(2)函数名也是变量
那么函数名是什么呢?函数名其实就是指向函数的变量!对于abs()这个函数,完全可以把函数名abs看成变量,它指向一个可以计算绝对值的函数!
如果把abs指向其他对象,会有什么情况发生?
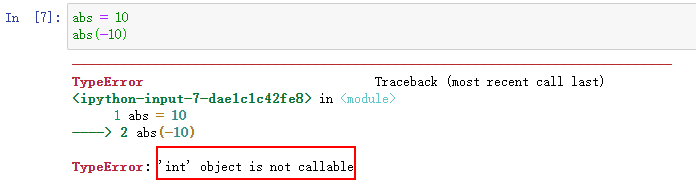
把abs指向10后,就无法通过abs(-10)调用该函数了!因为abs这个变量已经不指向求绝对值函数而是指向一个整数10!
当然实际代码绝对不能这么写,这里是为了说明函数名也是变量。要恢复abs函数,请重启 Python 交互环境。
注:由于abs函数实际上是定义在import builtins模块中的,所以要让修改abs变量的指向在其它模块也生效,要用import builtins; builtins.abs = 10。
(3)传入函数
既然变量可以指向函数,函数的参数能接收变量,那么一个函数就可以接收另一个函数作为参数,这种函数就称之为高阶函数。
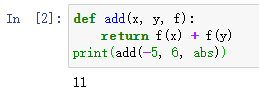
一个最简单的高阶函数:
def add(x, y, f):
return f(x) + f(y)当我们调用add(-5, 6, abs)时,参数x,y和f分别接收-5,6和abs,根据函数定义,我们可以推导计算过程为:
x = -5
y = 6
f = abs
f(x) + f(y) ==> abs(-5) + abs(6) ==> 11
return 11验证一下:
? 编写高阶函数,就是让函数的参数能够接收别的函数。
小结:
把函数作为参数传入,这样的函数称为高阶函数,函数式编程就是指这种高度抽象的编程范式。
4.2.1 map/reduce
Python 内建了map()和reduce()函数。
如果你读过 Google 的那篇大名鼎鼎的论文“MapReduce: Simplified Data Processing on Large Clusters”,你就能大概明白 map/reduce 的概念。
① map
我们先看 map。map()函数接收两个参数,一个是函数,一个是Iterable,map将传入的函数依次作用到序列的每个元素,并把结果作为新的Iterator返回。
举例说明,比如我们有一个函数 $ f(x)=x^2$,要把这个函数作用在一个 list [1, 2, 3, 4, 5, 6, 7, 8, 9]上,就可以用map()实现如下:
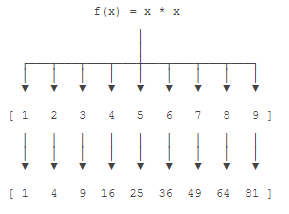
现在,我们用 Python 代码实现:
def f(x):
return x * x
r = map(f, [1, 2, 3, 4, 5, 6, 7, 8, 9])
list(r)
map()传入的第一个参数是f,即函数对象本身。由于结果r是一个Iterator,Iterator是惰性序列,因此通过list()函数让它把整个序列都计算出来并返回一个list。
你可能会想,不需要map()函数,写一个循环,也可以计算出结果:
L = []
for n in [1, 2, 3, 4, 5, 6, 7, 8, 9]:
L.append(f(n))
print(L)的确可以,但是,从上面的循环代码,能一眼看明白“把 f(x) 作用在 list 的每一个元素并把结果生成一个新的 list”吗?
所以,map()作为高阶函数,事实上它把运算规则抽象了,因此,我们不但可以计算简单的 $ f(x)=x^2$,还可以计算任意复杂的函数,比如,把这个 list 所有数字转为字符串:
list(map(str, [1, 2, 3, 4, 5, 6, 7, 8, 9]))
只需要一行代码。
② reduce
再看reduce的用法。reduce把一个函数作用在一个序列[x1, x2, x3, ...]上,这个函数必须接收两个参数,reduce把结果继续和序列的下一个元素做累积计算,其效果就是:
reduce(f, [x1, x2, x3, x4]) = f(f(f(x1, x2), x3), x4)比方说对一个序列求和,就可以用reduce实现:
from functools import reduce
def add(x, y):
return x + y
reduce(add, [1, 3, 5, 7, 9]) # 25当然求和运算可以直接用 Python 内建函数sum(),没必要动用reduce。
但是如果要把序列[1, 3, 5, 7, 9]变换成整数13579,reduce就可以派上用场:
from functools import reduce
def fn(x, y):
return x * 10 + y
reduce(fn, [1, 3, 5, 7, 9]) # 13579这个例子本身没多大用处,但是,如果考虑到字符串str也是一个序列,对上面的例子稍加改动,配合map(),我们就可以写出把str转换为int的函数:
from functools import reduce
def fn(x, y):
return x * 10 + y
def char2num(s):
digits = {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9}
return digits[s]
reduce(fn, map(char2num, '13579')) # 13579整理成一个str2int的函数就是:
from functools import reduce
DIGITS = {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9}
def str2int(s):
def fn(x, y):
return x * 10 + y
def char2num(s):
return DIGITS[s]
return reduce(fn, map(char2num, s))还可以用 lambda 函数进一步简化成:
from functools import reduce
DIGITS = {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9}
def char2num(s):
return DIGITS[s]
def str2int(s):
return reduce(lambda x, y: x * 10 + y, map(char2num, s))也就是说,假设 Python 没有提供int()函数,你完全可以自己写一个把字符串转化为整数的函数,而且只需要几行代码!
练习题:
【第一题】利用map()函数,把用户输入的不规范的英文名字,变为首字母大写,其他小写的规范名字。输入:['adam', 'LISA', 'barT'],输出:['Adam', 'Lisa', 'Bart']:
def normalize(name):
return name[0].upper() + name[1:].lower()或者也挺好:
def normalize(name):
return name.title() #title()函数 首字母大写 其他字母小写或者也挺好:
def normalize(name):
return name.capitalize()测试:
# 测试:
L1 = ['adam', 'LISA', 'barT']
L2 = list(map(normalize, L1))
print(L2)【第二题】Python 提供的sum()函数可以接受一个 list 并求和,请编写一个prod()函数,可以接受一个 list 并利用reduce()求积:
from functools import reduce
def prod(L):
return reduce(lambda x, y: x * y, L)测试:
print('3 * 5 * 7 * 9 =', prod([3, 5, 7, 9]))
if prod([3, 5, 7, 9]) == 945:
print('测试成功!')
else:
print('测试失败!')【第三题】利用map和reduce编写一个str2float函数,把字符串'123.456'转换成浮点数123.456:
法一:
from functools import reduce
def str2float(s):
digits = {'0': 0, '1': 1, '2': 2, '3': 3, '4': 4, '5': 5, '6': 6, '7': 7, '8': 8, '9': 9}
def char2num(c):
return digits[c]
def fn(x, y):
return x * 10 + y
pos = s.find('.')
if pos >= 0:
return (reduce(fn, map(char2num, s[:pos])) + reduce(fn, map(char2num, s[pos + 1:])) * (10 ** -len(s[pos + 1:])))
return reduce(fn, map(char2num, s))法二:
from functools import reduce
DIGITS = {'0':0, '1':1, '2':2, '3':3, '4':4, '5':5, '6':6, '7':7, '8':8, '9':9}
def str2float(s):
def str2num(s):
return DIGITS[s]
def fn(x, y):
return x * 10 + y
if '.' in s:
nPos = s.find('.')
s1 = s[:nPos]
s2 = s[nPos+1:]
n1 = reduce(fn, map(str2num, s1))
n2 = reduce(fn, map(str2num, s2))
return n1 + 0.1 ** len(s2) * n2
else:
return ruduce(fn, map(str2num, s))测试:
print('str2float(\'123.456\') =', str2float('123.456'))
if abs(str2float('123.456') - 123.456) < 0.00001:
print('测试成功!')
else:
print('测试失败!')4.2.2 filter
Python 内建的filter()函数用于过滤序列。
和map()类似,filter()也接收一个函数和一个序列。和map()不同的是,filter()把传入的函数依次作用于每个元素,然后根据返回值是True还是False决定保留还是丢弃该元素。
例如,在一个 list 中,删掉偶数,只保留奇数,可以这么写:
def is_odd(n):
return n % 2 == 1
list(filter(is_odd, [1, 2, 4, 5, 6, 9, 10, 15]))
# 结果: [1, 5, 9, 15]把一个序列中的空字符串删掉,可以这么写:
def not_empty(s):
return s and s.strip()
list(filter(not_empty, ['A', '', 'B', None, 'C', ' ']))
# 结果: ['A', 'B', 'C']可见用filter()这个高阶函数,关键在于正确实现一个“筛选”函数。
注意到filter()函数返回的是一个Iterator,也就是一个惰性序列,所以要强迫filter()完成计算结果,需要用list()函数获得所有结果并返回list。
① 用 filter 求素数
首先,列出从2开始的所有自然数,构造一个序列:
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
取序列的第一个数2,它一定是素数,然后用2把序列的2的倍数筛掉:
3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
取新序列的第一个数3,它一定是素数,然后用3把序列的3的倍数筛掉:
5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
取新序列的第一个数5,然后用5把序列的5的倍数筛掉:
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
不断筛下去,就可以得到所有的素数。
用 Python 来实现这个算法,可以先构造一个从3开始的奇数序列:
def _odd_iter():
n = 1
while True:
n = n + 2
yield n注意这是一个生成器,并且是一个无限序列。
然后定义一个筛选函数:
def _not_divisible(n):
return lambda x: x % n > 0最后,定义一个生成器,不断返回下一个素数:
def primes():
yield 2
it = _odd_iter() # 初始序列
while True:
n = next(it) # 返回序列的第一个数
yield n
it = filter(_not_divisible(n), it) # 构造新序列这个生成器先返回第一个素数2,然后,利用filter()不断产生筛选后的新的序列。
由于primes()也是一个无限序列,所以调用时需要设置一个退出循环的条件:
# 打印1000以内的素数:
for n in primes():
if n < 1000:
print(n)
else:
break注意到Iterator是惰性计算的序列,所以我们可以用 Python 表示“全体自然数”,“全体素数”这样的序列,而代码非常简洁。
练习题:
回数是指从左向右读和从右向左读都是一样的数,例如12321,909。请利用filter()筛选出回数:
def is_palindrome(n):
return str(n) == str(n)[::-1]测试:
# 测试:
output = filter(is_palindrome, range(1, 1000))
print('1~1000:', list(output))
if list(filter(is_palindrome, range(1, 200))) == [1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191]:
print('测试成功!')
else:
print('测试失败!')小结:
filter()的作用是从一个序列中筛出符合条件的元素。由于filter()使用了惰性计算,所以只有在取filter()结果的时候,才会真正筛选并每次返回下一个筛出的元素。
4.2.3 sorted
① 排序算法
排序也是在程序中经常用到的算法。无论使用冒泡排序还是快速排序,排序的核心是比较两个元素的大小。如果是数字,我们可以直接比较,但如果是字符串或者两个 dict呢?直接比较数学上的大小是没有意义的,因此,比较的过程必须通过函数抽象出来。
Python 内置的sorted()函数就可以对 list 进行排序:
sorted([36, 5, -12, 9, -21])
此外,sorted()函数也是一个高阶函数,它还可以接收一个key函数来实现自定义的排序,例如按绝对值大小排序:
sorted([36, 5, -12, 9, -21], key=abs)
key 指定的函数将作用于 list 的每一个元素上,并根据 key 函数返回的结果进行排序。对比原始的 list 和经过key=abs处理过的 list:
list = [36, 5, -12, 9, -21]
keys = [36, 5, 12, 9, 21]然后sorted()函数按照 keys 进行排序,并按照对应关系返回 list 相应的元素:

我们再看一个字符串排序的例子:
sorted(['bob', 'about', 'Zoo', 'Credit'])
默认情况下,对字符串排序,是按照 ASCII 的大小比较的,由于'Z' < 'a',结果,大写字母Z会排在小写字母a的前面。
现在,我们提出排序应该忽略大小写,按照字母序排序。要实现这个算法,不必对现有代码大加改动,只要我们能用一个 key 函数把字符串映射为忽略大小写排序即可。忽略大小写来比较两个字符串,实际上就是先把字符串都变成大写(或者都变成小写),再比较。
这样,我们给sorted传入 key 函数,即可实现忽略大小写的排序:
sorted(['bob', 'about', 'Zoo', 'Credit'], key=str.lower)
要进行反向排序,不必改动 key 函数,可以传入第三个参数reverse=True:
sorted(['bob', 'about', 'Zoo', 'Credit'], key=str.lower, reverse=True)
从上述例子可以看出,高阶函数的抽象能力是非常强大的,而且,核心代码可以保持得非常简洁。
小结:
sorted()也是一个高阶函数。用sorted()排序的关键在于实现一个映射函数。
练习题:
假设我们用一组 tuple 表示学生名字和成绩:
L = [('Bob', 75), ('Adam', 92), ('Bart', 66), ('Lisa', 88)]请用sorted()对上述列表分别按名字升序排序,再按成绩从高到低排序。
(1)按名字升序排序
L = [('Bob', 75), ('Adam', 92), ('Bart', 66), ('Lisa', 88)]
def by_name(t):
return t[0]
L2 = sorted(L, key=by_name)
print(L2)
(2)按成绩从高到低排序
L = [('Bob', 75), ('Adam', 92), ('Bart', 66), ('Lisa', 88)]
def by_name(t):
return -t[1]
L2 = sorted(L, key=by_name)
print(L2)
4.3 返回函数
4.3.1 函数作为返回值
高阶函数除了可以接受函数作为参数外,还可以把函数作为结果值返回。
我们来实现一个可变参数的求和。通常情况下,求和的函数是这样定义的:
def calc_sum(*args):
ax = 0
for n in args:
ax = ax + n
return ax但是,如果不需要立刻求和,而是在后面的代码中,根据需要再计算怎么办?可以不返回求和的结果,而是返回求和的函数:
def lazy_sum(*args):
def sum():
ax = 0
for n in args:
ax = ax + n
return ax
return sum当我们调用lazy_sum()时,返回的并不是求和结果,而是求和函数:
>>> f = lazy_sum(1, 3, 5, 7, 9)
>>> f
<function lazy_sum.<locals>.sum at 0x101c6ed90>调用函数f时,才真正计算求和的结果:
>>> f()
25
在这个例子中,我们在函数lazy_sum中又定义了函数sum,并且,内部函数sum可以引用外部函数lazy_sum的参数和局部变量,当lazy_sum返回函数sum时,相关参数和变量都保存在返回的函数中,这种称为“闭包(Closure)”的程序结构拥有极大的威力。
请再注意一点,当我们调用lazy_sum()时,每次调用都会返回一个新的函数,即使传入相同的参数:
>>> f1 = lazy_sum(1, 3, 5, 7, 9)
>>> f2 = lazy_sum(1, 3, 5, 7, 9)
>>> f1==f2
False
>>> f1()==f2()
Truef1()和f2()的调用结果互不影响。
4.3.2 闭包
注意到返回的函数在其定义内部引用了局部变量args,所以,当一个函数返回了一个函数后,其内部的局部变量还被新函数引用,所以,闭包用起来简单,实现起来可不容易。
另一个需要注意的问题是,返回的函数并没有立刻执行,而是直到调用了f()才执行。我们来看一个例子:
def count():
fs = []
for i in range(1, 4):
def f():
return i*i
fs.append(f)
return fs
f1, f2, f3 = count()在上面的例子中,每次循环,都创建了一个新的函数,然后,把创建的 3 个函数都返回了。
你可能认为调用f1(),f2()和f3()结果应该是1,4,9,但实际结果是:
>>> f1()
9
>>> f2()
9
>>> f3()
9全部都是9!原因就在于返回的函数引用了变量i,但它并非立刻执行。等到 3 个函数都返回时,它们所引用的变量i已经变成了3,因此最终结果为9。
如果一定要引用循环变量怎么办?方法是再创建一个函数,用该函数的参数绑定循环变量当前的值,无论该循环变量后续如何更改,已绑定到函数参数的值不变:
def count():
def f(j):
def g():
return j*j
return g
fs = []
for i in range(1, 4):
fs.append(f(i)) # f(i)立刻被执行,因此i的当前值被传入f()
return fs再看看结果:
>>> f1, f2, f3 = count()
>>> f1()
1
>>> f2()
4
>>> f3()
9缺点是代码较长,可利用 lambda 函数缩短代码。
练习题:
利用闭包返回一个计数器函数,每次调用它返回递增整数:
- 法一:
def createCounter():
i = 0
def counter():
nonlocal i #这句声明是闭包函数应用同名变量的重点。
while True:
i = i + 1
return i
return counter- 法二:
# 选择数值可变但是地址不变的变量类型——数组
def createCounter():
i = [0] # 初始化数组
def counter():
i[0] += 1 #不修改数组, 尽修改数组中元素数值, 数组的地址不变
return i[0]
return counter- 法三:
# 也可以选择dict类型变量,与数组同理, 主要不改变变量引用地址即可
def createCounter():
i = {'a':0}
def counter():
i['a'] += 1
return i['a']
return counter- 测试:
# 测试:
counterA = createCounter()
print(counterA(), counterA(), counterA(), counterA(), counterA()) # 1 2 3 4 5
counterB = createCounter()
if [counterB(), counterB(), counterB(), counterB()] == [1, 2, 3, 4]:
print('测试通过!')
else:
print('测试失败!')小结:
一个函数可以返回一个计算结果,也可以返回一个函数。
返回一个函数时,牢记该函数并未执行,返回函数中不要引用任何可能会变化的变量。
4.4 匿名函数
当我们在传入函数时,有些时候,不需要显式地定义函数,直接传入匿名函数更方便。
在 Python 中,对匿名函数提供了有限支持。还是以map()函数为例,计算 $f(x)=x^2$ 时,除了定义一个f(x)的函数外,还可以直接传入匿名函数:
list(map(lambda x: x * x, [1, 2, 3, 4, 5, 6, 7, 8, 9]))通过对比可以看出,匿名函数lambda x: x * x实际上就是:
def f(x):
return x * x关键字lambda表示匿名函数,冒号前面的x表示函数参数。
匿名函数有个限制,就是只能有一个表达式,不用写return,返回值就是该表达式的结果。
用匿名函数有个好处,因为函数没有名字,不必担心函数名冲突。此外,匿名函数也是一个函数对象,也可以把匿名函数赋值给一个变量,再利用变量来调用该函数:
>>> f = lambda x: x * x
>>> f
<function <lambda> at 0x101c6ef28>
>>> f(5)
25同样,也可以把匿名函数作为返回值返回,比如:
def build(x, y):
return lambda: x * x + y * y练习题:
请用匿名函数改造下面的代码:
def is_odd(n):
return n % 2 == 1
L = list(filter(is_odd, range(1, 20)))
print(L)用匿名函数改造:
L = list(filter(lambda x: x %2 == 1, range(1, 20)))
print(L)那如果用列表生成式改造呢?
L = [x for x in range(1,20) if x % 2 == 1]
print(L)小结:
Python 对匿名函数的支持有限,只有一些简单的情况下可以使用匿名函数。
4.5 装饰器
由于函数也是一个对象,而且函数对象可以被赋值给变量,所以,通过变量也能调用该函数。
def now():
print('2020-07-19')
f = now
f() # 结果:2020-07-19函数对象有一个__name__属性,可以拿到函数的名字:
>>> now.__name__
'now'
>>> f.__name__
'now'现在,假设我们要增强now()函数的功能,比如,在函数调用前后自动打印日志,但又不希望修改now()函数的定义,这种在代码运行期间动态增加功能的方式,称之为“装饰器”(Decorator)。
本质上,decorator 就是一个返回函数的高阶函数。所以,我们要定义一个能打印日志的 decorator,可以定义如下:
def log(func):
def wrapper(*args, **kw):
print('call %s():' % func.__name__)
return func(*args, **kw)
return wrapper观察上面的log,因为它是一个 decorator,所以接受一个函数作为参数,并返回一个函数。我们要借助 Python 的 @ 语法,把 decorator 置于函数的定义处:
@log
def now():
print('2020-07-19')调用now()函数,不仅会运行now()函数本身,还会在运行now()函数前打印一行日志:
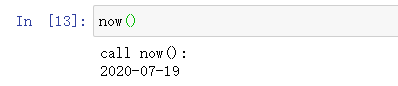
把@log放到now()函数的定义处,相当于执行了语句:
now = log(now)由于log()是一个 decorator,返回一个函数,所以,原来的now()函数仍然存在,只是现在同名的now变量指向了新的函数,于是调用now()将执行新函数,即在log()函数中返回的wrapper()函数。
wrapper()函数的参数定义是(*args, **kw),因此,wrapper()函数可以接受任意参数的调用。在wrapper()函数内,首先打印日志,再紧接着调用原始函数。
如果 decorator 本身需要传入参数,那就需要编写一个返回 decorator 的高阶函数,写出来会更复杂。比如,要自定义 log 的文本:
def log(text):
def decorator(func):
def wrapper(*args, **kw):
print('%s %s():' % (text, func.__name__))
return func(*args, **kw)
return wrapper
return decorator这个 3 层嵌套的 decorator 用法如下:
@log('execute')
def now():
print('2020-07-19')执行结果如下:
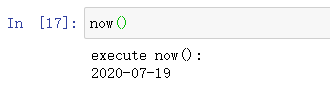
和两层嵌套的 decorator 相比,3 层嵌套的效果是这样的:
>>> now = log('execute')(now)我们来剖析上面的语句,首先执行log('execute'),返回的是decorator函数,再调用返回的函数,参数是now函数,返回值最终是wrapper函数。
以上两种 decorator 的定义都没有问题,但还差最后一步。因为我们讲了函数也是对象,它有__name__等属性,但你去看经过 decorator 装饰之后的函数,它们的__name__已经从原来的'now'变成了'wrapper':
>>> now.__name__
'wrapper'因为返回的那个wrapper()函数名字就是'wrapper',所以,需要把原始函数的__name__等属性复制到wrapper()函数中,否则,有些依赖函数签名的代码执行就会出错。
不需要编写wrapper.__name__ = func.__name__这样的代码,Python 内置的functools.wraps就是干这个事的,所以,一个完整的 decorator 的写法如下:
import functools
def log(func):
@functools.wraps(func)
def wrapper(*args, **kw):
print('call %s():' % func.__name__)
return func(*args, **kw)
return wrapper或者针对带参数的 decorator:
import functools
def log(text):
def decorator(func):
@functools.wraps(func)
def wrapper(*args, **kw):
print('%s %s():' % (text, func.__name__))
return func(*args, **kw)
return wrapper
return decoratorimport functools是导入functools模块。模块的概念稍候讲解。现在,只需记住在定义wrapper()的前面加上@functools.wraps(func)即可。
练习题:
请设计一个 decorator,它可作用于任何函数上,并打印该函数的执行时间:
import time, functools
def metric(fn):
@functools.wraps(fn)
def wrapper(*args, **kw):
start_time = time.time()
e = fn(*args, **kw)
end_time = time.time()
print('%s executed in %s ms' % (fn.__name__, end_time - start_time))
return e
return wrapper测试:
# 测试
@metric
def fast(x, y):
time.sleep(0.0012)
return x + y;
@metric
def slow(x, y, z):
time.sleep(0.1234)
return x * y * z;
f = fast(11, 22)
s = slow(11, 22, 33)
if f != 33:
print('测试失败!')
elif s != 7986:
print('测试失败!')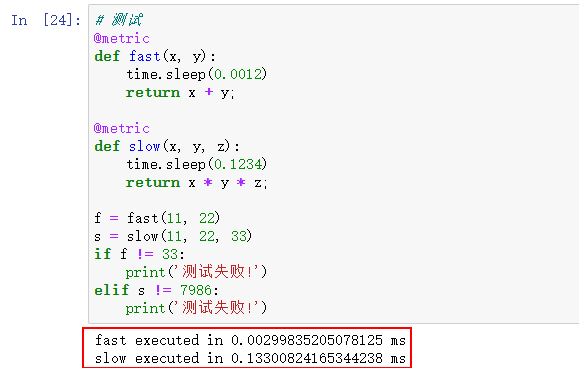
小结:
在面向对象(OOP)的设计模式中,decorator 被称为装饰模式。OOP 的装饰模式需要通过继承和组合来实现,而 Python 除了能支持 OOP 的 decorator 外,直接从语法层次支持 decorator。Python 的 decorator 可以用函数实现,也可以用类实现。
decorator 可以增强函数的功能,定义起来虽然有点复杂,但使用起来非常灵活和方便。
再思考一下能否写出一个@log的 decorator,使它既支持:
@log
def f():
pass又支持:
@log('execute')
def f():
passeg.
def log(text):
if isinstance(text, str):
def decorator(func):
@functools.wraps(func)
def wrapper(*args, **kw):
print('%s %s(): ' % (text, func.__name__))
return func(*args, **kw)
return wrapper
return decorator
def wrapper(*args, **kw):
print('%s %s(): ' % (text, func.__name__))
return func(*args, **kw)
return wrapper4.6 偏函数
Python 的functools模块提供了很多有用的功能,其中一个就是偏函数(Partial function)。要注意,这里的偏函数和数学意义上的偏函数不一样。
在介绍函数参数的时候,我们讲到,通过设定参数的默认值,可以降低函数调用的难度。而偏函数也可以做到这一点。举例如下:
int()函数可以把字符串转换为整数,当仅传入字符串时,int()函数默认按十进制转换:
>>> int('12345')
12345但int()函数还提供额外的base参数,默认值为10。如果传入base参数,就可以做 N 进制的转换:
>>> int('12345', base=8)
5349
>>> int('12345', 16)
74565假设要转换大量的二进制字符串,每次都传入int(x, base=2)非常麻烦,于是,我们想到,可以定义一个int2()的函数,默认把base=2传进去:
def int2(x, base=2):
return int(x, base)这样,我们转换二进制就非常方便了:
>>> int2('1000000')
64
>>> int2('1010101')
85functools.partial就是帮助我们创建一个偏函数的,不需要我们自己定义int2(),可以直接使用下面的代码创建一个新的函数int2:
>>> import functools
>>> int2 = functools.partial(int, base=2)
>>> int2('1000000')
64
>>> int2('1010101')
85所以,简单总结functools.partial的作用就是,把一个函数的某些参数给固定住(也就是设置默认值),返回一个新的函数,调用这个新函数会更简单。
注意到上面的新的int2函数,仅仅是把base参数重新设定默认值为2,但也可以在函数调用时传入其他值:
>>> int2('1000000', base=10)
1000000最后,创建偏函数时,实际上可以接收函数对象、*args和**kw这 3 个参数,当传入:
int2 = functools.partial(int, base=2)实际上固定了 int() 函数的关键字参数base,也就是:
int2('10010')相当于:
kw = { 'base': 2 }
int('10010', **kw)当传入:
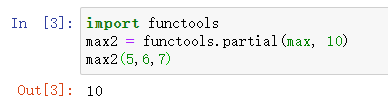
max2 = functools.partial(max, 10)实际上会把10作为*args的一部分自动加到左边,也就是:
max2(5, 6, 7)相当于:
args = (10, 5, 6, 7)
max(*args)结果为10。
小结:
当函数的参数个数太多,需要简化时,使用functools.partial可以创建一个新的函数,这个新函数可以固定住原函数的部分参数,从而在调用时更简单。
